 In geometry, a cardioid (from Greek καρδιά (kardiá) 'heart') is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius.
In geometry, a cardioid (from Greek καρδιά (kardiá) 'heart') is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius.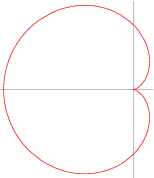 The cardioid has a cusp at the origin. The name cardioid was first used by de Castillon in Philosophical Transactions of the Royal Society in 1741. Its arc length was found by la Hire in 1708. There are exactly three parallel tangents to the cardioid with any given gradient.
The cardioid has a cusp at the origin. The name cardioid was first used by de Castillon in Philosophical Transactions of the Royal Society in 1741. Its arc length was found by la Hire in 1708. There are exactly three parallel tangents to the cardioid with any given gradient. The cardioid, a name first used by de Castillon in a paper in the Philosophical Transactions of the Royal Societyin 1741, is a curve that is the locus of a point on the circumference of circle rolling round the circumference of a circle of equal radius.
The cardioid, a name first used by de Castillon in a paper in the Philosophical Transactions of the Royal Societyin 1741, is a curve that is the locus of a point on the circumference of circle rolling round the circumference of a circle of equal radius.